Simple spirals
While playing with Python Turtle, I came across drawing simple spirals with polygons rotating within themselves. I liked how we could get so many patterns by making small changes to the code.
Here is an example of such spirals:
 |
| Simple spirals |
Here is the
code to draw the spirals shown above:
Note: You can run, edit and make your own changes to all the code samples in this post and try them out (thanks to trinket).
Expected shapes
Though I liked the output of this code, it seemed a bit irregular. I wanted to see the polygons rotating inside one another in a regular pattern with the vertices touching the edges of the outer polygon.
Here is an example of what I wanted to see:
 |
| Expected shapes |
Simple polygons
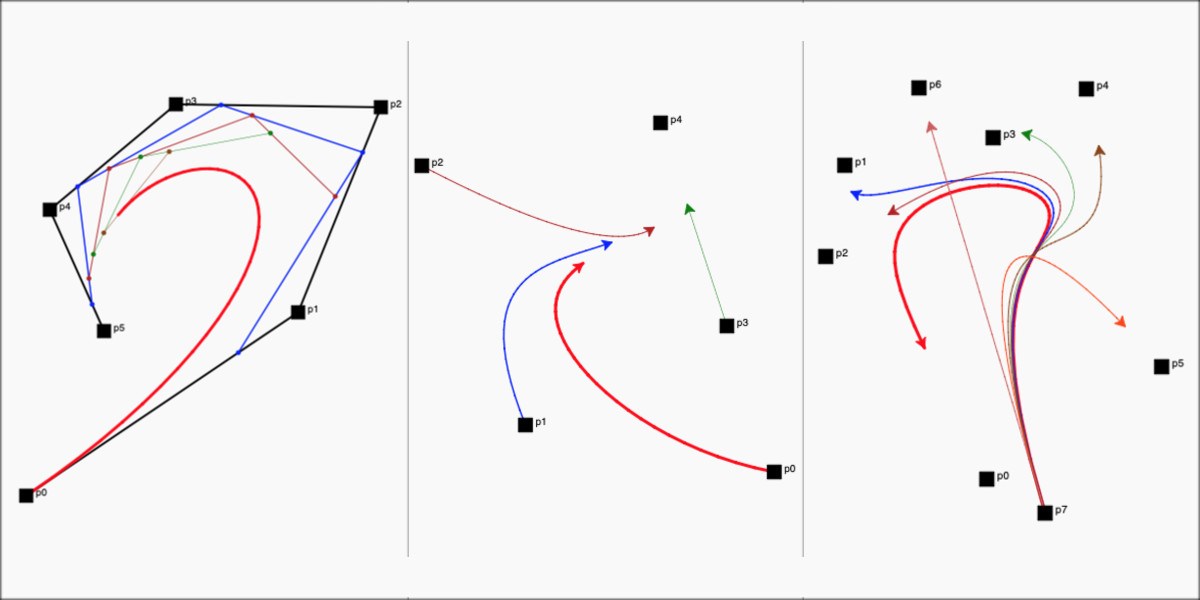
The above image shows that we can rotate the shapes around a given centre point. So, I wanted to first draw regular polygons around a given centre point. To do that, I had to calculate the starting point (sx, sy in image below) to draw the polygon using Turtle. I used the following
link to calculate this. As shown in the link, I had to calculate the 'radius' and angle 'a' for a polygon first as shown in the image below.
 |
| Method to get starting point |
Here is the output of the simple polygons drawn around the given centres:
 |
| Simple polygons |
Here is the
code to draw the simple polygons shown above:
Polygon spirals
Now that we have a regular polygon, I wanted to rotate it around the same centre and create the spirals shown before. To do that, I had to first calculate the rotated starting point (rsx, rsy shown in image below) and the angle 'a' to know where to start the Turtle and with what angle to draw the new polygon. I used the reference from this
link to do this.
 |
| Method to get rotated starting point |
Then, I had to reduce the length of the polygon side as it rotates inside. The new length has to be such that the rotated polygon fits perfectly in the previous polygon. The angle by which the polygons rotate inside is constant. The length of the rotating polygons reduce by a fixed factor every time.
Here is the output that I got after doing this:
 |
| Polygon spirals |
Here is the
code for the polygon spirals shown above:
Here is how these polygon spirals look when filled alternatively:
 |
| Filled polygon spirals |
I then tried to rotate the polygons in the opposite direction and also draw the base polygon at different angles with respect to the x-axis.
Here is an example output of a triangle spiral. The second spiral is in the opposite direction to the first. The third one is rotated 180 degrees from x-axis. See image below:
 |
| Reversed and rotated spirals |
Here is the
code for the reversed and rotated spirals shown above:
Tiles
Now that I am able to draw regular polygon spirals with any number of sides any where on the screen in any direction with any starting angle with respect to x-axis, I wanted try and see if there are interesting patterns when they are tiled in some regular fashion.
Here is how I thought we could put some polygon spirals to create some basic tiles:
 |
| Tiles from individual spirals |
I created some simple patterns based on the rotated angle and direction of the spirals.
Here is the output of a few tiles. The first two are from individual triangle spirals and the next two are from individual square spirals. See image below:
 |
| Tiles |
Here is the
code for the tiles shown above:
Here is how these tiles look when filled alternatively:
 |
| Filled tiles |
Here is an example of a partial hexagon tiling comprised of other smaller hexagon spirals:
 |
| A partial tiling with hexagon spirals |
Tilings
Now that we have interesting tiles, I wanted to see how it looked if we tiled the entire screen with these.
Here are some sample outputs of such tilings I could get:
 |
| A tiling with triangle spirals |
|
 |
| A tiling with square spirals |
|
Here is the
code for the tilings shown above and the image at the very top of this post:
(You can comment/uncomment the last few lines to try these out)
Here is how these tilings look when filled alternatively:
 |
| A filled tiling |
 |
| Another filled tiling |
Summary
In summary, polygons in polygons create very interesting spirals and shapes.
All the code in this post is available on
GitHub.
Updates:
7 June 2020
- I learnt that these rotating polygons in polygons are also called as Whirls. I also learnt that the vertices follow a path as described in the mice problem. This is probably why these are also called as pursuit polygons as the vertices move in pursuit of each other.
- Added alternatively filled images
5 July 2020
- An interactive version of Polygon Whirls can be found in this later post.
- Pardhav Maradani