Bézier Curve Animations

In a previous post about Trees, I used straight lines and parts of circles to create curves.  Since then, I am learning more about curves and came across Bézier curves.  I liked the animations shown in the Wikipedia link and wondered if I could draw them using Python Turtle.

I also wanted to make this interactive where I could pause and resume the animations, add more control points, move them anywhere on the screen, etc.

Bézier Curve Animation

The actual construction of Bézier curves as mentioned on Wikipedia is straight forward and uses something called De Casteljau's algorithm.  It is a recursive method as follows:

For N control points:

• We have N - 1 initial segments connecting them
• For each t between 0 and 1, we connect points that are t times the length of the segment.  We now get N - 1 control points and N - 2 segments between them
• We repeat the previous step till we have one point, which is the terminating condition for our recursive function

Please see the 'get_bezier_point' function in the code shown below for this implementation.

I then added buttons using different Python Turtles with custom shapes for play / pause, increment and decrement control points.

To be able to move the control points, I decided to use different Turtles for each control point.  I soon realised that there was a problem in distinguishing which control point was being clicked and dragged.  I think this is a problem specific to Trinket (but I am not sure).  So, I then learnt about how to create a custom Turtle using Classes and extend it.  This gave me the ability to clearly identify each control point.  Please see the 'ControlPoint' Class in the code shown below.

When we drag and move the control points, we have to redraw the Bézier curve upto the current t value (shown in 'red' in the image below).  This is a special case.  Other than that, we draw the connecting line segments as described in the algorithm above.

Here is an example animation of the output that I got once I did this:

Bézier curve animation

Here is the code for the above:

Note: You can run, edit and make your own changes to all the code samples in this post and try them out (thanks to trinket).  Each run produces a different random output in all the examples below.  You can play / pause the animation, add / delete control points, click and drag them.

Relation to Pursuit Curves

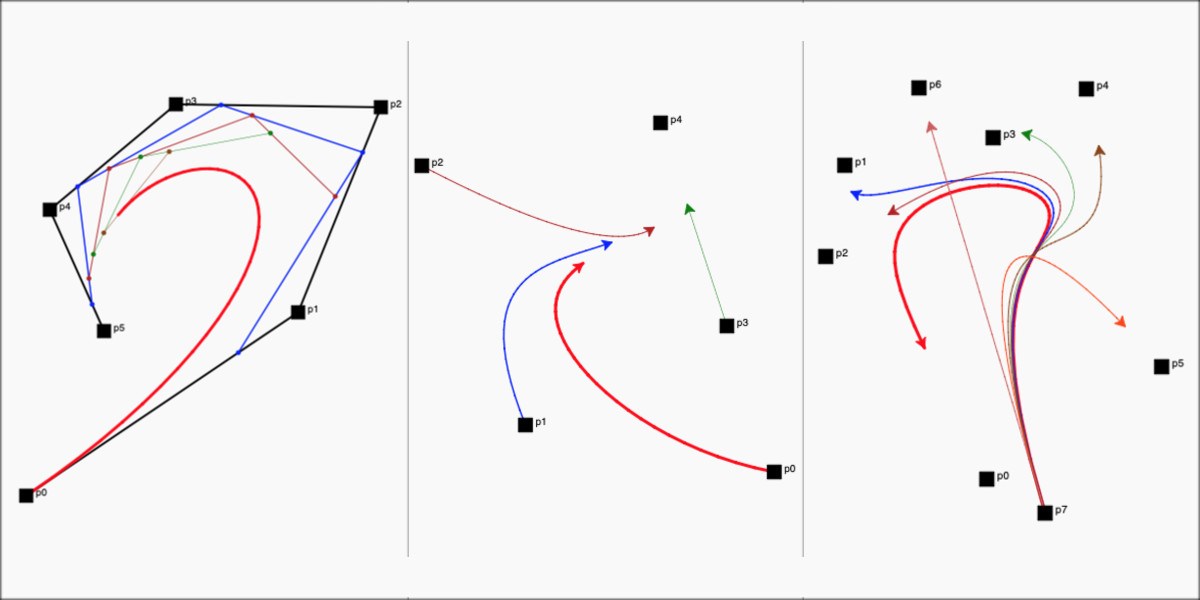
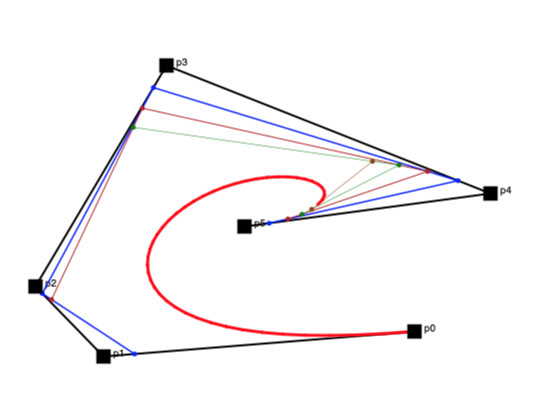
Towards the end of a previous post (Polygons in Polygons), I mentioned about Pursuit polygons, mice problem, etc.  Looking at the animations above, I noticed quite a lot of similarity with those as the lines were in pursuit of one another.  To show this more clearly, I drew the points of the curve from each of the control points which were in pursuit of the other curves which were emerging from the next control point.

Here is a reference Bézier curve that I will use to illustrate:

Bézier curves in pursuit reference

Here is an animation to illustrate the pursuit behaviour of the same curve shown above:

Bézier curves in pursuit

As you can see from the animation above, the actual Bézier curve (which is shown in 'red' starting from p0), is essentially in pursuit of the curve starting from p1 (in blue), which itself is in pursuit of the curve starting from p2 (in firebrick), etc, etc.  I used the default Turtle shape to show where they are headed.  The curve from the last but one to the last control point is always a straight line (p4 to p4 above) as can be seen above as well.

I see a lot of similarity to Pursuit curves (and mice problem, etc), but didn't see this mentioned elsewhere.

Here is the code for the above:

Diverging Bézier Curves

After that, I wanted to reverse the direction of the curves to see how this looks.  Instead of all curves converging at one point, we should now see all curves starting at one point (last control point) and diverging from there to their respective control points.

Here is an example animation of this:

Diverging Bézier curves

This looks like something we could use to trace the path of fireworks launched from a single source, etc.  All the curves reach their destination at the same time but follow different curved paths to get there.  

Here is the code for the above animations:

(There is a variable called 'g_shuffle' in the code below that you can set to True to randomise the curves while keeping the control points the same.)

Relation to Rotating Polygons

When I first saw the Bézier curve animations, I saw a similarity to rotating polygons in polygons that I wrote about in a previous post.  There, I was using a fixed offset to move along the outer edge of a polygon to draw the inner rotated polygon and repeat it.  This is similar to what is happening here in the algorithm mentioned before in the construction of Bézier curves, but done recursively.

I made minor changes to generate these rotating polygons using the same code to generate Bézier curves as shown below.

Here is an example animation of an irregular polygon rotating within itself towards the centre:

Rotating spirals

Here is the code for the above:

Summary

In summary, Bézier curves are very interesting.  We can relate them to a lot of other things.  I can see using them in the future for a variety of things.

All the code in this post is available on GitHub.

Updates:

5 July 2020

1. An interactive version of all the example here can be found in this later post.

- Pardhav Maradani